Big data et cerveau : la neurobiologie computationnelle
David Holcman, directeur de Recherche au CNRS, dirige un groupe de biologie computationnelle et de mathématiques appliquées à l’École normale supérieure (membre de l'Université PSL). Son groupe développe des méthodes de calculs, de modélisation et d’analyse de données pour la biologie cellulaire et moléculaire, et ses applications médicales.
De nouveaux outils de modélisation pour la neurobiologie
Depuis plus de 150 ans, les grandes avancées en neurobiologie sont venues de l’expérimentation, notamment grâce au microscope. Avec un grossissement de 100 et un esprit déductif, Louis Pasteur et ses collaborateurs ont, en deux générations, compris les modes de propagation infectieux et décrit l’hygiène moderne.
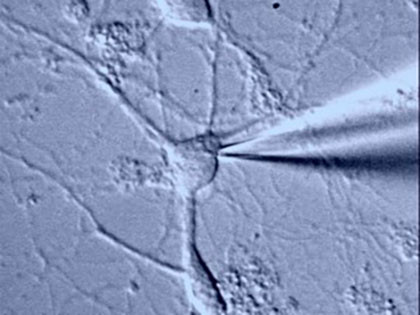
Le développement rapide de l’électrophysiologie, en Angleterre, en 1950, a ensuite permis d’enregistrer l’électricité des neurones, à l’aide de micropipettes contenant des solutions salines. Enfin, grâce aux microscopes modernes, nous pouvons aujourd’hui descendre à la résolution du nanomètre dans l’observation des cellules vivantes.
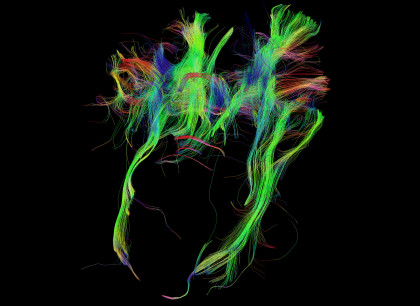
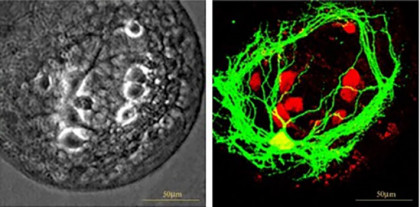
Malgré ces progrès, la complexité du vivant est telle que l’on n’a pas encore identifié de principe fonctionnel ou d'organisation simple en biologie, comme la conservation de l’énergie en physique, par exemple. En effet, l’organisation à l’échelle de la molécule influence grandement la cellule, qui influence elle-même l’organe entier. Ainsi, dans le cerveau s’entremêlent des réseaux de neurones, des astrocytes (cellules du système nerveux central) et des vaisseaux sanguins en constante interaction. Pour décoder le fonctionnement du cerveau, qui soutient la perception, la pensée, l’action, la mémoire, et la décision, nous utilisons aujourd'hui des modèles mathématiques.
Si l’on compare le cerveau à un ordinateur, ces modèles visent à modéliser et imiter « le matériel », ou hardware (les interactions entre molécules et cellules) mais aussi le « logiciel », ou software, (le code neuronal, c’est-à-dire la « langue » dans laquelle le cerveau transmet l’information, qui n’est pas encore élucidé). La neurobiologie reste un challenge pour les mathématiques et la physique statistique, car il faut à la fois prendre en compte la complexité du vivant, et trouver des méthodes et algorithmes qui permettent d’obtenir des résultats convaincants pour expliquer et prédire les lois neuronales.
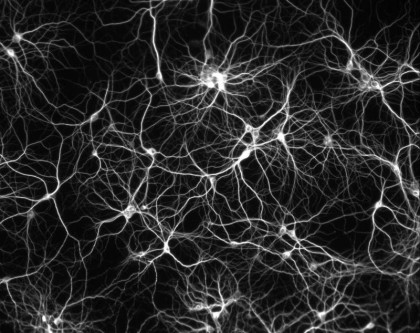
Organisation d’un neurone
La biophysique des neurones est compliquée car elle dépend de processus très variés : les molécules sont acheminées depuis le lieu de leur production vers leur destination finale par différents modes de transport, eux aussi régulés par de nombreux facteurs, internes et externes à la cellule.
Ainsi, certains mécanismes actifs de transport des ions (sorte d’échangeurs à la surface des cellules) définissent le voltage du neurone. Celui-ci n’est jamais constant : il dépend des canaux de transport mais aussi des cellules voisines.
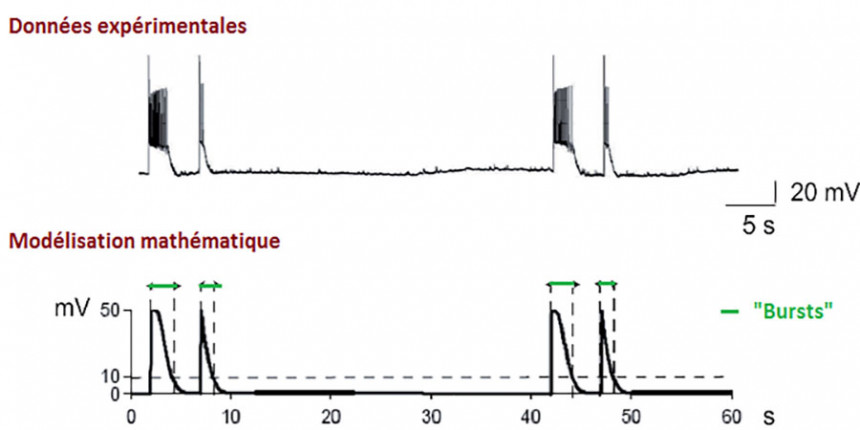
Ces changements déterminent l’activité du neurone et participent à l’activité du réseau dans lequel il s’inscrit. Les neurones, cellules excitables, peuvent moduler leur activité électrique, qui se présente parfois comme oscillante, parfois sous forme de bouffées persistantes.
Qu’apporte la modélisation à l’étude du cerveau ?
La modélisation sert de cadre pour les calculs et l’analyse des propriétés, de la molécule aux réseaux de neurones. Les simulations numériques des équations biophysiques imitent ce qui se passe pendant quelques millisecondes dans un microvolume, à l’échelle du nanomètre.
La modélisation permet par exemple de calculer la probabilité d’un échange d’information réussi d’un neurone à l’autre, ou d’étudier des phénomènes inaccessibles à l’observation : comment un petit réseau de neurones garde-t-il en mémoire l’activité du passé proche ?
La modélisation mathématique révèle par exemple que l’activité des synapses permet d’expliquer la mémoire d’un réseau de neurones sur une durée de 30 secondes.
L'approche de la modélisation clarifie en outre les procédés par lesquels la cellule est stimulée par le monde extérieur et lui répond. Elle nous permet par exemple de définir les conditions nécessaires pour qu’une petite concentration de calcium en transit dans une synapse change le poids d’un neurone et son influence sur le neurone voisin auquel il est connecté. À grande échelle, nous utilisons la modélisation pour étudier l’organisation des oscillations neuronales en décharges périodiques qui déclenchent la respiration.
Par ailleurs, après une décharge électrique neuronale, des ions potassium sont expulsés d’un neurone, mais où vont-ils et comment se recyclent-ils ? Il est important de le comprendre car, si le potassium s’accumule, le système neuronal peut perdre son équilibre naturel, donnant lieu à une dérive vers des comportements épileptiques.
L’étude des échanges moléculaires pendant l’apprentissage a quant à elle donné naissance à la théorie du « petit trou ». Puis l’analyse de centaines de milliers de petites trajectoires, développée pour la première fois dans notre laboratoire à l’IBENS, a révélé de nouvelles structures organisées dans les synapses, d’une taille de l’ordre de 100 nanomètres, qui seraient déterminantes dans les processus d’apprentissage au niveau moléculaire.
Une aide à la prédiction médicale
Avoir un modèle mathématique permet d’extraire des paramètres précis. Comme pour la météo, un bon modèle permet de prédire le temps sur une semaine. Par conséquent, avoir un bon modèle du cœur ou de l’activité neuronale pourrait permettre de prévenir des accidents comme les infarctus ou les AVC.
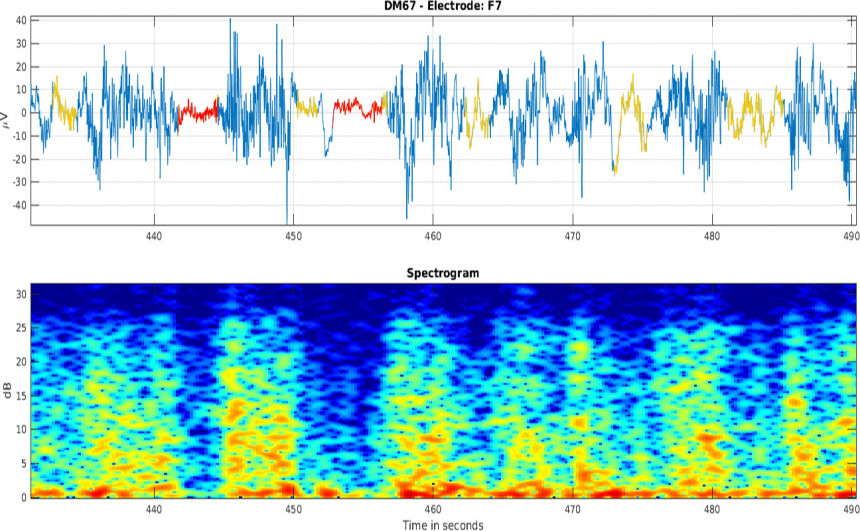
Récemment, l’analyse du signal d’électroencéphalogrammes, combinée avec l’analyse des données médicales des patients, nous a permis de prédire le taux de survie à un arrêt cardio-respiratoire ou des comportements à risque pendant une anesthésie.
Biologie, médecine et big data
La modélisation et les simulations numériques sont une composante indispensable du Big data. Elles vont transformer la statistique de classification ou le machine-learning automatique en modèles de prédiction, ce qui permettra d’évoluer vers une médecine préventive et individuelle. C’est aussi, sans doute, une nouvelle économie qui est en train de naître dans les mains des chercheurs. Ce scénario semble récemment repris par le gouvernement qui met l’accent sur l’intelligence artificielle comme un pilier de la recherche.
Bibliographie
David Holcman est directeur de Recherche au CNRS, et dirige un groupe de biologie computationnelle et de mathématiques appliquées à l' IBENS (UMR8197, ENS-CNRS-Inserm). Il est aussi membre du Churchill College à Cambridge.
Voir les publications scientifiques de David Holcman sur PSL-Explore, en particulier :
- D. Holcman Z. Schuss, Stochastic Narrow Escape in Molecular and Cellular Biology, Monographs, Springer 260 p 2015, sur PSL-Explore et sur le site de Springer.
- J. Cartailler T.Know, R. Yuste D. Holcman, Deconvolution of voltage sensor time series and electro-diffusion modeling of synaptic input in dendritic spines, Neuron, 2018 ;97(5):1126-1136 2018.
- D. Holcman, Z. Schuss, Asymptotics of Elliptic and Parabolic PDEs and their Applications in Statistical Physics, Computational Neuroscience, and Biophysics, Applied mathematics Series, Springer, 2018.
Tribunes libres :
- D. Holcman, "La nouvelle Physique-Mathématique pour décrypter la biologie cellulaire et booster l’économie de haute technologie"
- D. Holcman, "Comment l'économie High Tech peut émerger sans refondre le système universitaire", sur Mediapart.
Vidéo de vulgarisation grand public sur les grands principes et enjeux de l'épigénétique.
Le cerveau de la souris pourrait compenser les mauvaises informations reçues de l'environnement.
Cette conférence expérimentale proposée par l'ESPCI met en évidence l'activité des neurones dans les circuits moteurs responsables du mouvem